Inférence bayésienne
Lors du développement de Datice, Bénédicte Lemieux-Dudon s’est basée sur l’approche et le vocabulaire introduit par Mosegaard et Tarantola, 20021K. Mosegaard and A. Tarantola. International Handbook of Earthquake and Engineering Seismology (Part A). Chapter : Probabilistic Approach to Inverse Problems. Academic Press, 2002. Avant d’appliquer le théorème de Bayes à notre problème, il est nécessaire d’introduire différentes définitions.
Tout d’abord, les observations ![]() et les paramètres du modèle
et les paramètres du modèle ![]() sont des grandeurs physiques qui peuvent être considérées comme des variables aléatoires et donc définies par une densité de probabilité. On définit une densité de probabilité homogène (indicé
sont des grandeurs physiques qui peuvent être considérées comme des variables aléatoires et donc définies par une densité de probabilité. On définit une densité de probabilité homogène (indicé ![]() ) lorsque qu’aucune information a priori ne permet d’établir un lien entre les variables aléatoires
) lorsque qu’aucune information a priori ne permet d’établir un lien entre les variables aléatoires ![]() et
et ![]() . Elle est notée
. Elle est notée ![]() . Au couple de variables aléatoires
. Au couple de variables aléatoires ![]() est associé une densité de probabilité jointe
est associé une densité de probabilité jointe ![]() qui décrit les corrélations possibles entre
qui décrit les corrélations possibles entre ![]() et
et ![]() , ainsi que les incertitudes associées au modèle théorique de façon symétrique Tarantola, 20052Albert Tarantola. Inverse Problem Theory and Methods for Model Parameter Estimation. Society for Industrial and Applied Mathematics, 2005. . Il est possible que les informations a priori ne soient pas complètement indépendantes. Il n’est pas exclu qu’une partie des observations
, ainsi que les incertitudes associées au modèle théorique de façon symétrique Tarantola, 20052Albert Tarantola. Inverse Problem Theory and Methods for Model Parameter Estimation. Society for Industrial and Applied Mathematics, 2005. . Il est possible que les informations a priori ne soient pas complètement indépendantes. Il n’est pas exclu qu’une partie des observations ![]() ait contribué à produire les paramètres d’ébauche
ait contribué à produire les paramètres d’ébauche ![]() . On introduit alors la densité de probabilité jointe des informations a priori:
. On introduit alors la densité de probabilité jointe des informations a priori: ![]() où l’indice
où l’indice ![]() fait référence à l’ébauche (« background » en anglais).
fait référence à l’ébauche (« background » en anglais).
L’objectif de cette modélisation inverse est de trouver une valeur vraie à ![]() en se basant sur les informations a priori à notre disposition. Afin de simplifier l’écriture du théorème de Bayes, nous allons maintenant présenter les hypothèses sur lesquelles repose l’inférence bayésienne:
en se basant sur les informations a priori à notre disposition. Afin de simplifier l’écriture du théorème de Bayes, nous allons maintenant présenter les hypothèses sur lesquelles repose l’inférence bayésienne:
- Dissymétrie des rôles de
 et
et 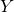 dans le modèle théorique direct.
dans le modèle théorique direct.
Le qualificatif « direct » signifie que l’on cherche la probabilité d’avoir une mesure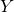 connaissant la valeur de
connaissant la valeur de  (
(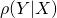 ). Ceci conduit à la réécriture de la densité de probabilité conditionnelle:
). Ceci conduit à la réécriture de la densité de probabilité conditionnelle:
(1) ![]()
- Indépendance de l’information a priori et des observations.
On introduit alors les densités de probabilité associées à l’ébauche (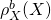 ) et aux observations (
) et aux observations (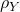 ). Dans ce cas, la densité de probabilité jointe
). Dans ce cas, la densité de probabilité jointe 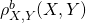 s’écrit:
s’écrit:
(2) ![]()
- La limite homogène de la densité de probabilité jointe.
En utilisant la limite homogène de la densité de probabilité jointe (équation 2), il est possible de décomposer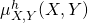 en deux densités de probabilité homogènes
en deux densités de probabilité homogènes 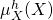 et
et 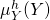 :
:
(3) ![]()
Afin d’obtenir l’état d’information a posteriori ![]() , Mosegaard et Tarantola, 20023K. Mosegaard and A. Tarantola. International Handbook of Earthquake and Engineering Seismology (Part A). Chapter : Probabilistic Approach to Inverse Problems. Academic Press, 2002 s’appuient sur l’opération de conjonction de probabilité simplifiée dans le cadre de l’inférence bayésienne:
, Mosegaard et Tarantola, 20023K. Mosegaard and A. Tarantola. International Handbook of Earthquake and Engineering Seismology (Part A). Chapter : Probabilistic Approach to Inverse Problems. Academic Press, 2002 s’appuient sur l’opération de conjonction de probabilité simplifiée dans le cadre de l’inférence bayésienne:
(4) 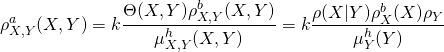
avec ![]() une constante de normalisation.
une constante de normalisation.
En intégrant cette équation sur l’espace des observations (![]() ), on obtient l’expression de l’information a posteriori sur
), on obtient l’expression de l’information a posteriori sur ![]() :
:
(5) ![]()
Dans le but d’obtenir un contrôle optimal sur ![]() , on introduit la notion de fonction coût,
, on introduit la notion de fonction coût, ![]() , qui traduit les contraintes du problème imposées à
, qui traduit les contraintes du problème imposées à ![]() . Cette fonction coût mesure la distance entre les observations
. Cette fonction coût mesure la distance entre les observations ![]() et la prédiction du modèle. L’optimalité est obtenue lorsque le critère de maximum de vraisemblance selon Mosegaard et Tarantola, 20024K. Mosegaard and A. Tarantola. International Handbook of Earthquake and Engineering Seismology (Part A). Chapter : Probabilistic Approach to Inverse Problems. Academic Press, 2002 est atteint. Ce critère d’optimalité peut se traduire par la recherche du minimum de la fonction coût:
et la prédiction du modèle. L’optimalité est obtenue lorsque le critère de maximum de vraisemblance selon Mosegaard et Tarantola, 20024K. Mosegaard and A. Tarantola. International Handbook of Earthquake and Engineering Seismology (Part A). Chapter : Probabilistic Approach to Inverse Problems. Academic Press, 2002 est atteint. Ce critère d’optimalité peut se traduire par la recherche du minimum de la fonction coût:
(6) ![]()
(7) ![]()
Définition des âges glace et gaz
Les âges glace et gaz en fonction de la profondeur sont déterminés à partir de trois grandeurs glaciologiques:
- le taux d’accumulation
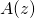 ,
, - la fonction d’amincissement
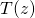 ,
, - la profondeur de piégeage de l’air en équivalent glace (LIDIE)
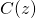 .
.
Le taux d’accumulation correspond à la quantité de neige précipitée à la surface de la calotte sur l’année. Il est généralement exprimé en ![]() ou son équivalent en glace
ou son équivalent en glace ![]() . La fonction d’amincissement est définie comme le rapport entre l’épaisseur réelle d’une couche annuelle à la profondeur
. La fonction d’amincissement est définie comme le rapport entre l’épaisseur réelle d’une couche annuelle à la profondeur ![]() et son épaisseur d’origine lors de son dépôt en surface en équivalent glace. La fonction d’amincissement est donc sans unité. On peut directement relier l’épaisseur d’une couche annuelle au taux d’accumulation et à la fonction d’amincissement:
et son épaisseur d’origine lors de son dépôt en surface en équivalent glace. La fonction d’amincissement est donc sans unité. On peut directement relier l’épaisseur d’une couche annuelle au taux d’accumulation et à la fonction d’amincissement: ![]() .
.
Ainsi, la relation profondeur-âge d’une carotte de glace correspond à l’intégrale de l’inverse de l’épaisseur de couche annuelle. On définit l’âge glace ![]() comme:
comme:
(8) ![]()
avec ![]() la densité relative du matériau (neige/glace) par rapport à la glace:
la densité relative du matériau (neige/glace) par rapport à la glace: ![]() .
.
Pour pouvoir calculer l’âge du gaz, ![]() , il est nécessaire de connaître la différence de profondeur entre du gaz et de la glace ayant le même âge, appelée
, il est nécessaire de connaître la différence de profondeur entre du gaz et de la glace ayant le même âge, appelée ![]() . Ce
. Ce ![]() va donc correspondre à la profondeur de piégeage de l’air au moment du dépôt, qui a ensuite subi un amincissement lors de son enfouissement jusqu’à la profondeur
va donc correspondre à la profondeur de piégeage de l’air au moment du dépôt, qui a ensuite subi un amincissement lors de son enfouissement jusqu’à la profondeur ![]() (équation ref{eq_ddepth}). On en déduit donc l’âge du gaz à la profondeur
(équation ref{eq_ddepth}). On en déduit donc l’âge du gaz à la profondeur ![]() comme étant l’âge de la glace à la profondeur
comme étant l’âge de la glace à la profondeur ![]() (équation 10).
(équation 10).
(9) ![]()
(10) ![]()
On définit aussi ce qu’on appelle le ![]() comme étant la différence d’âge entre la glace et le gaz à une même profondeur:
comme étant la différence d’âge entre la glace et le gaz à une même profondeur:
(11) ![]()
Formulation du modèle d’inversion
Fonctions de correction
Nous avons vu dans la section précédente les différents paramètres glaciologiques nécessaires pour le calcul des âges gaz et glace : le taux d’accumulation, la fonction d’amincissement et la LIDIE. L’objectif de Datice est d’améliorer les ébauches de ces paramètres par modélisation inverse. L’inversion se fait simultanément sur ![]() forages où chaque forage
forages où chaque forage ![]() (
(![]() ) possède des ébauches pour le taux d’accumulation (
) possède des ébauches pour le taux d’accumulation (![]() ), la fonction d’amincissement (
), la fonction d’amincissement (![]() ) et la LIDIE (
) et la LIDIE (![]() ). Datice cherche à obtenir de nouvelles estimations de ces paramètres glaciologiques sous la forme de corrections des ébauches:
). Datice cherche à obtenir de nouvelles estimations de ces paramètres glaciologiques sous la forme de corrections des ébauches:
(12) ![]()
(13) ![]()
(14) ![]()
où les fonctions ![]() ,
, ![]() et
et ![]() sont respectivement les fonctions de correction pour l’accumulation, l’amincissement et la LIDIE. Datice cherche alors à déterminer les fonctions de correction optimales simultanément pour chacun des forages. A partir de cela, l’outil est en mesure de calculer les paramètres glaciologiques optimisés
sont respectivement les fonctions de correction pour l’accumulation, l’amincissement et la LIDIE. Datice cherche alors à déterminer les fonctions de correction optimales simultanément pour chacun des forages. A partir de cela, l’outil est en mesure de calculer les paramètres glaciologiques optimisés ![]() ,
, ![]() et
et ![]() , également appelés grandeurs analysées. Datice peut ensuite en déduire les chronologies gaz et glace optimales pour chacun des forages.
, également appelés grandeurs analysées. Datice peut ensuite en déduire les chronologies gaz et glace optimales pour chacun des forages.
Ainsi, le vecteur ![]() , qui représente les paramètres du modèle, est caractérisé par les fonctions de correction des trois paramètres glaciologiques pour chacun des forages:
, qui représente les paramètres du modèle, est caractérisé par les fonctions de correction des trois paramètres glaciologiques pour chacun des forages:
(15) 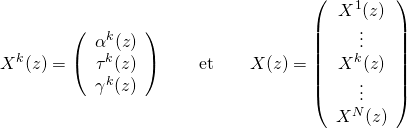
Le vecteur ![]() est ce qu’on appelle la variable d’état du problème inverse.
est ce qu’on appelle la variable d’état du problème inverse.
Par leur nature, et par les définitions 8 et 10 qui permettent de calculer les âges glace et gaz, le taux d’accumulation, la fonction d’amincissement et la LIDIE ne peuvent prendre que des valeurs strictement positives. De ce fait, les phénomènes tels que l’érosion en surface par le vent, conduisant à une accumulation négative, ou encore le retournement de couches de glace au cours de l’écoulement ne sont pas pris en compte. Ces contraintes sur les grandeurs glaciologiques se propagent aussi sur les fonctions de correction. Ainsi, les composantes du vecteur ![]() sont toutes strictement positives.
sont toutes strictement positives.
Changement de variable
Du fait que les paramètres caractérisant le vecteur ![]() soient strictement positifs, les composantes du vecteur
soient strictement positifs, les composantes du vecteur ![]() sont alors mieux décrites par des densités de probabilité lognormales.
sont alors mieux décrites par des densités de probabilité lognormales.
Les grandeurs ![]() et
et ![]() caractérisant les ébauches sont donc assimilées à la médiane et à une mesure de dispersion.
caractérisant les ébauches sont donc assimilées à la médiane et à une mesure de dispersion.
Comme il est plus facile de travailler avec des densités de probabilité gaussiennes, on effectue le changement de variable suivant:
(16) ![]()
(17) ![]()
Ainsi, le vecteur d’ébauche ![]() correspond à la moyenne/médiane/mode de la distribution et
correspond à la moyenne/médiane/mode de la distribution et ![]() la matrice de covariance d’erreur d’ébauche.
la matrice de covariance d’erreur d’ébauche.
La variable de contrôle du problème est alors ![]() . Le développement de la fonction coût et l’optimisation du problème se font donc à partir de
. Le développement de la fonction coût et l’optimisation du problème se font donc à partir de ![]() .
.
Les paramètres d’ébauches
Il nous est possible de déterminer la valeur du vecteur d’ébauche dans l’espace de contrôle, ![]() , en nous intéressant au vecteur
, en nous intéressant au vecteur ![]() puisque ces deux vecteurs sont reliés par la relation 17. Au regard de la définition des fonctions de correction, le vecteur
puisque ces deux vecteurs sont reliés par la relation 17. Au regard de la définition des fonctions de correction, le vecteur ![]() est défini au travers de l’information a priori dont on dispose sur les paramètres glaciologiques. Rappelons que ces grandeurs (
est défini au travers de l’information a priori dont on dispose sur les paramètres glaciologiques. Rappelons que ces grandeurs (![]() ,
, ![]() et
et ![]() ) sont obtenues à l’aide de modèles glaciologiques et correspondent aux valeurs les plus probables des grandeurs
) sont obtenues à l’aide de modèles glaciologiques et correspondent aux valeurs les plus probables des grandeurs ![]() ,
, ![]() et
et ![]() a priori. En terme de vecteur d’ébauche, ceci se traduit par:
a priori. En terme de vecteur d’ébauche, ceci se traduit par:
(18) ![]()
La matrice de covariance d’erreur d’ébauche ![]() associée à la carotte de glace
associée à la carotte de glace ![]() mesure les variances et les covariances d’erreur a priori sur le vecteur d’ébauche
mesure les variances et les covariances d’erreur a priori sur le vecteur d’ébauche ![]() . Cette matrice est de la forme:
. Cette matrice est de la forme:
(19) 
Les blocs diagonaux correspondent aux covariances d’erreur sur ![]() ,
, ![]() et
et ![]() . Les blocs non-diagonaux rendent compte des covariances d’erreur croisées entre
. Les blocs non-diagonaux rendent compte des covariances d’erreur croisées entre ![]() ,
, ![]() et
et ![]() . On se restreint aux cas de matrices
. On se restreint aux cas de matrices ![]() inversibles en faisant l’hypothèse que la matrice
inversibles en faisant l’hypothèse que la matrice ![]() est définie strictement positive.
est définie strictement positive.
Dans le cadre des applications présentées dans cette thèse, les hypothèses suivantes ont été considérées:
- pas de corrélation d’erreur entre les scénarios d’ébauche de 2 carottes de glace différentes,
- pas de corrélation d’erreur entre
 ,
,  et
et  pour une même carotte.
pour une même carotte.
De ce fait, la matrice ![]() est seulement composée des blocs diagonaux
est seulement composée des blocs diagonaux ![]() associés à chaque forage:
associés à chaque forage:
(20) 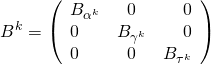
(21) ![]()
(22) ![]()
(23) ![]()
Les écart-types ![]() ,
, ![]() et
et ![]() sont déduits à partir de l’analyse des erreurs commises sur les paramètres d’ébauche
sont déduits à partir de l’analyse des erreurs commises sur les paramètres d’ébauche ![]() ,
, ![]() et
et ![]() respectivement. On rappelle que ces paramètres sont généralement obtenus grâce à des modèles glaciologiques.
respectivement. On rappelle que ces paramètres sont généralement obtenus grâce à des modèles glaciologiques.
Dans le cas de l’accumulation et la LIDIE, l’hypothèse de non-corrélation d’erreur est discutable. En effet, ces deux grandeurs étant liées, leurs fonctions de correction devraient présenter une corrélation entre elles.
Les observations
Datice peut prendre en compte différents types d’observations pour contraindre les chronologies. On peut les classer en deux groupes:
- les marqueurs d’âge et de grandeurs qui ne contraignent qu’une seule carotte de glace (marqueurs d’âge glace et gaz, marqueurs de
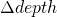 ).
). - les liens stratigraphiques définis entre deux carottes de glace (gaz et glace).
Ainsi, il est possible de décomposer le vecteur d’observation sous la forme:
(24) ![]()
Avec ![]() le vecteur regroupant les contraintes spécifiques à un seul forage, et
le vecteur regroupant les contraintes spécifiques à un seul forage, et ![]() celui regroupant les observations se rapportant à un couple de carottes.
celui regroupant les observations se rapportant à un couple de carottes.
Plusieurs hypothèses sont faites quant aux incertitudes associées à ces observations dans le cadre du problème inverse:
- les densités de probabilité des différentes observations sont correctement décrites par des gaussiennes,
- les incertitudes sur les marqueurs d’âge et de grandeurs sont indépendantes entre les forages,
- les incertitudes sur les liens stratigraphiques sont indépendantes entre les forages,
- les incertitudes sur les marqueurs appliqués à un forage et sur un couple de forages sont indépendantes,
- les incertitudes des différents marqueurs sont toutes indépendantes les unes des autres,
- les incertitudes sur les profondeurs des observations sont négligeables devant les incertitudes sur les mesures.
Toutes ces hypothèses permettent de séparer les densités de probabilité de ![]() et
et ![]() en produit de densités marginales, simplifiant la dérivation de la fonction coût.
en produit de densités marginales, simplifiant la dérivation de la fonction coût.
Pour la suite, on a besoin de définir l’opérateur d’observation généralisé ![]() . Ce vecteur permet, étant donnée une valeur pour le vecteur de contrôle
. Ce vecteur permet, étant donnée une valeur pour le vecteur de contrôle ![]() , de prédire le vecteur d’observation
, de prédire le vecteur d’observation ![]() moyennant une erreur:
moyennant une erreur:
(25) ![]()
Du fait de la décomposition faite précédemment du vecteur ![]() , l’opérateur d’observation s’écrit:
, l’opérateur d’observation s’écrit:
(26) ![]()
De plus, on fait l’hypothèse que les incertitudes théoriques associées au modèle directe sont négligeables par rapport aux incertitudes de mesure.
Fonction coût et minimisation
Fonction coût
Comme chaque forage possède sa propre discrétisation en fonction de la profondeur, le vecteur ![]() peut devenir très grand. En conséquence, il a été choisi que la densité de probabilité \textit{a posteriori} serait déterminée à l’aide du critère d’optimalité de maximum de vraisemblance qui fait intervenir la notion de fonction coût
peut devenir très grand. En conséquence, il a été choisi que la densité de probabilité \textit{a posteriori} serait déterminée à l’aide du critère d’optimalité de maximum de vraisemblance qui fait intervenir la notion de fonction coût ![]() .Comme chaque forage possède sa propre discrétisation en fonction de la profondeur, le vecteur
.Comme chaque forage possède sa propre discrétisation en fonction de la profondeur, le vecteur ![]() peut devenir très grand. En conséquence, il a été choisi que la densité de probabilité \textit{a posteriori} serait déterminée à l’aide du critère d’optimalité de maximum de vraisemblance qui fait intervenir la notion de fonction coût
peut devenir très grand. En conséquence, il a été choisi que la densité de probabilité \textit{a posteriori} serait déterminée à l’aide du critère d’optimalité de maximum de vraisemblance qui fait intervenir la notion de fonction coût ![]() .
.
Sous les hypothèses de l’inversion bayésienne, la fonction coût peut se décomposer en un terme d’ébauche et un terme associé aux observations.
(27) ![]()
La fonction coût détaillée pour toutes les observations prises en compte par Datice s’écrit alors:
(28) ![Rendered by QuickLaTeX.com \begin{equation*} J (\tilde{X}) & = \sum ^N_{k=1} \frac{1}{2} \left( \tilde{X}_k - \tilde{X}_k^b \right) ^T [\mathbf{B}]^{-1} \left( \tilde{X}_k - \tilde{X}_k^b \right) + \sum ^N_{k=1} \frac{1}{2} \left( Y^{ii}_k - \mathbf{h}_k^{ii} ( \tilde{X}_k ) \right) ^T [\mathbf{R}^{ii}_k]^{-1} \left( Y^{ii}_k - \mathbf{h}_k^{ii} ( \tilde{X}_k ) \right) \end{equation*}](https://datice-multi-archives.ipsl.fr/wp-content/ql-cache/quicklatex.com-eb2dedd7a1922e4bbc49cb429c7a107c_l3.png)
Dans l’équation 28, le premier terme correspond à l’ébauche, et le second terme représente de façon abrégé les différents types d’observation (où ![]() peut correspondre aux marqueurs de
peut correspondre aux marqueurs de ![]() , aux marqueurs d’âge glace, aux marqueurs d’âge gaz , aux liens stratigraphiques glace et gaz tous les autres marqueurs intégrés dans Datice).
, aux marqueurs d’âge glace, aux marqueurs d’âge gaz , aux liens stratigraphiques glace et gaz tous les autres marqueurs intégrés dans Datice).
Minimisation
Afin d’obtenir le vecteur ![]() optimisé, le critère de maximum de vraisemblance impose de trouver le minimum de la fonction coût (équation 7). Pour ce faire, l’optimisation repose sur des méthodes numériques dites de descente. On cherche à se diriger vers le minimum de
optimisé, le critère de maximum de vraisemblance impose de trouver le minimum de la fonction coût (équation 7). Pour ce faire, l’optimisation repose sur des méthodes numériques dites de descente. On cherche à se diriger vers le minimum de ![]() , par itérations successives suivant un chemin de descente.
, par itérations successives suivant un chemin de descente.
Datice utilise le minimiseur m1qn3 (Gilbert et Lemaréchal, 1989)5J.-C. Gilbert and C. Lemaréchal. Some numerical experiments with variable-storage quasi-Newton algotithms. Mathematical Programming, 45 :407–435, 1989.. Il est adapté pour résoudre des problèmes de grande échelle peu contraints. Ce minimiseur repose sur la connaissance de la fonction à minimiser ainsi que son gradient afin de pouvoir approximer son hessien (matrice des dérivées secondes de la fonction). A partir de cela, il est possible de déduire la direction de descente de la minimisation pour la prochaine itération.
La minimisation est arrêtée lorsque le test sur le gradient est satisfait, c’est à dire lorsqu’on atteint une certaine précision définie par l’utilisateur (par exemple, la valeur demandée pour Datice est ![]() ). Ce critère est basé sur la norme du gradient de la fonction coût :
). Ce critère est basé sur la norme du gradient de la fonction coût :
![]()
avec ![]() le gradient de la fonction coût de la
le gradient de la fonction coût de la ![]() ème itération et
ème itération et ![]() celui de la première itération.
celui de la première itération.
Nouvelle chronologie optimisée
Une fois le test du gradient satisfait, ou presque satisfait dans certains cas, Datice détermine le vecteur ![]() regroupant les fonctions de correction optimales. En appliquant le changement de variable inverse, on obtient le vecteur
regroupant les fonctions de correction optimales. En appliquant le changement de variable inverse, on obtient le vecteur ![]() regroupant les fonctions de correction
regroupant les fonctions de correction ![]() ,
, ![]() et
et ![]() . L’outil de datation en déduit les grandeurs glaciologiques optimales puis les chronologies correspondantes, gaz et glace, pour chacun des forages. L’atout majeur de cette méthode de datation est qu’elle calcule directement l’incertitude associée aux chronologies.
. L’outil de datation en déduit les grandeurs glaciologiques optimales puis les chronologies correspondantes, gaz et glace, pour chacun des forages. L’atout majeur de cette méthode de datation est qu’elle calcule directement l’incertitude associée aux chronologies.
Erreur a posteriori sur 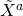
Suite à la minimisation, Datice est en mesure de calculer la matrice de covariance d’erreur a posteriori sur ![]() , en faisant l’hypothèse que l’opérateur d’observation généralisé est faiblement non linéaire:
, en faisant l’hypothèse que l’opérateur d’observation généralisé est faiblement non linéaire:
(29) ![]()
où ![]() est l’opérateur linéaire tangent associé à l’opérateur d’observation généralisé,
est l’opérateur linéaire tangent associé à l’opérateur d’observation généralisé, ![]() la matrice de covariance d’erreur d’ébauche généralisée (section ??) et
la matrice de covariance d’erreur d’ébauche généralisée (section ??) et ![]() la matrice de covariance d’erreur d’observation généralisée (section ??).
la matrice de covariance d’erreur d’observation généralisée (section ??).
Nous pouvons noter que les blocs diagonaux de la matrice ![]() donnent les écart-types \textit{a posteriori} sur les composantes de
donnent les écart-types \textit{a posteriori} sur les composantes de ![]() :
:
![]()
avec ![]() et
et ![]() les indices associés à chaque carotte de glace.
les indices associés à chaque carotte de glace.
Erreur a posteriori sur la chronologie
On rappelle que le changement de variable de ![]() à
à ![]() a permis de passer de distributions lognormales à gaussiennes. La seule quantité conservée entre ces deux distributions est la médiane. Afin de bien comprendre les étapes successives pour en arriver à l’estimation de l’erreur sur les chronologies analysées, nous allons raisonner sous forme d’intervalle de confiance.
a permis de passer de distributions lognormales à gaussiennes. La seule quantité conservée entre ces deux distributions est la médiane. Afin de bien comprendre les étapes successives pour en arriver à l’estimation de l’erreur sur les chronologies analysées, nous allons raisonner sous forme d’intervalle de confiance.
Ainsi, en considérant 1–sigma pour l’erreur a posteriori sur ![]() , cela correspond à un intervalle de confiance à 68\% . Si on prend l’exemple des grandeurs associées au taux d’accumulation, l’optimisation de
, cela correspond à un intervalle de confiance à 68\% . Si on prend l’exemple des grandeurs associées au taux d’accumulation, l’optimisation de ![]() pour la carotte de glace
pour la carotte de glace ![]() à une profondeur donnée nous permet de dire que l’on fait une erreur de l’ordre de 32 \% en affirmant :
à une profondeur donnée nous permet de dire que l’on fait une erreur de l’ordre de 32 \% en affirmant :
(30) ![]()
En appliquant le changement de variable inverse (![]() ), on en déduit l’intervalle de confiance à 68\% sur
), on en déduit l’intervalle de confiance à 68\% sur ![]() :
:
(31) ![]()
(32) ![]()
Après conversion en accumulation, en utilisant la relation ![]() de la section ??, cela devient:
de la section ??, cela devient:
(33) ![]()
(34) ![]()
La même démarche s’applique pour la fonction d’amincissement et la LIDIE afin d’en déduire leurs intervalles de confiance à 68\% .
L’incertitude sur l’âge est donc fonction de nombreux facteurs. En considérant que tous ces facteurs sont statistiquement indépendants, on peut faire l’hypothèse que les incertitudes sur les chronologies optimales pour chaque site ![]() sont correctement décrites par des gaussiennes.
sont correctement décrites par des gaussiennes.
Le vecteur de l’âge de la glace en fonction de la profondeur pour chaque forage est obtenu à partir de la relation 8. On définit la matrice de covariance d’erreur \textit{a posteriori} ![]() associée à la chronologie glace
associée à la chronologie glace ![]() comme:
comme:
(35) ![]()
où ![]() est l’opérateur linéaire tangent du modèle d’âge glace.
est l’opérateur linéaire tangent du modèle d’âge glace.
La matrice ![]() est symétrique et ses blocs diagonaux donnent les covariances d’erreur associées à chacun des
est symétrique et ses blocs diagonaux donnent les covariances d’erreur associées à chacun des ![]() forages. L’intervalle de confiance de chacune des chronologies glace optimales est directement donné par les éléments diagonaux de la matrice
forages. L’intervalle de confiance de chacune des chronologies glace optimales est directement donné par les éléments diagonaux de la matrice ![]() . Pour le forage
. Pour le forage ![]() ayant une grille de profondeur
ayant une grille de profondeur ![]() , l’erreur sur l’âge glace à la profondeur
, l’erreur sur l’âge glace à la profondeur ![]() correspond à:
correspond à:
(36) ![]()
References
| ↑1, ↑3, ↑4 | K. Mosegaard and A. Tarantola. International Handbook of Earthquake and Engineering Seismology (Part A). Chapter : Probabilistic Approach to Inverse Problems. Academic Press, 2002 |
|---|---|
| ↑2 | Albert Tarantola. Inverse Problem Theory and Methods for Model Parameter Estimation. Society for Industrial and Applied Mathematics, 2005. |
| ↑5 | J.-C. Gilbert and C. Lemaréchal. Some numerical experiments with variable-storage quasi-Newton algotithms. Mathematical Programming, 45 :407–435, 1989. |